Probability Distribution Calculators: |
 |
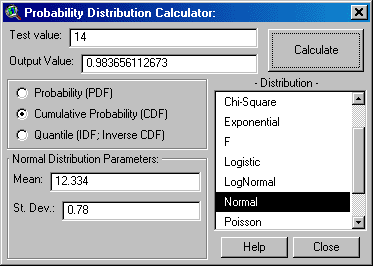
This extension includes two versions of a Probability
Distribution Calculator, each of which calculate distribution data based on a
variety of distributions and parameters. The Probability Distribution
Calculator is started from within a View, and is opened by clicking on the
button in the View toolbar.
You simply enter the input and parameter values, specify whether you are
calculating Probability, Cumulative Probability or Quantile values, and
click “Calculate”, and the result appears in the “Output Value” window.
This calculator stays open until you close it and you can leave it open as
you do other things in ArcView.
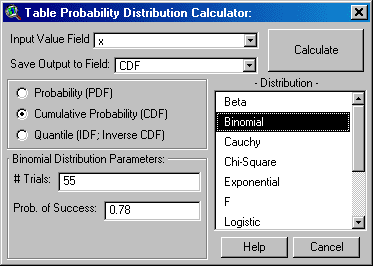
The “Table Probability Distribution Calculator” is
designed to work on all selected records in a table, applying the
distribution parameters to each value and saving the results to a field in
that table. This calculator is opened from within a Table by clicking on
the button in the Table
toolbar. Select the field containing the “Input” values, then decide
whether to create a new field or use an existing field to save the
“Output" values, then click “Calculate” to generate distribution values
for all selected records.The window stays open until you click “Calculate”
or “Cancel”.
The Distribution functions included with this extension may be grouped in 3 categories. In general, the Probability Density Functions return the probability that the Test Value = X, given that particular distribution. The Cumulative Distribution Functions return the probability that the Test Value <= X, given that particular distribution. The Quantile Functions (sometimes referred to as Inverse Density Functions or Percent Point Functions) return the Value X at which P(X) = [specified cumulative probability], given that particular distribution.
|
Functions and Probability Distributions |
|||
|
Distribution |
Probability Density Function |
Cumulative Distribution Function |
Quantile Function |
|
Beta |
PDF_Beta |
CDF_Beta |
IDF_Beta |
|
Binomial |
PDF_Binomial |
CDF_Binomial |
IDF_Binomial |
|
Cauchy |
PDF_Cauchy |
CDF_Cauchy |
IDF_Cauchy |
|
Chi-Square |
PDF_ChiSquare |
CDF_ChiSquare |
IDF_ChiSquare |
|
Exponential |
PDF_Exp |
CDF_Exp |
IDF_Exp |
|
F |
PDF_F |
CDF_F |
IDF_F |
|
Logistic |
PDF_Logistic |
CDF_Logistic |
IDF_Logistic |
|
LogNormal |
PDF_LogNormal |
CDF_LogNormal |
IDF_LogNormal |
|
Normal |
PDF_Normal_Simpsons |
CDF_Normal |
IDF_Normal |
|
Poisson |
PDF_Poisson |
CDF_Poisson |
IDF_Poisson |
|
Student’s T |
PDF_StudentsT |
CDF_StudentsT |
IDF_StudentsT |
|
Weibull |
PDF_Weibull |
CDF_Weibull |
IDF_Weibull |
Equations for each function are included in the Discussions of Distribution Functions, Parameters and Usages, but some them do not have closed formulas that can be calculated and therefore must be computed numerically. The author refers interested persons to the references to find source code and computational methods of calculating these functions. The author especially recommends Croarkin & Tobias (date unknown) and McLaughlin (2001) for illustrations of the various distributions, and Press et al. (1988-1997) and Burkardt (2001) for computational methods. These sources are all available on-line.
The Discussions of Distribution Functions describe 4 methods of utilizing each function. The first method describes how to use the Probability Distribution Calculators to calculate values, and there are three additional methods available for programmers who want to access the functions through Avenue code. Simply copy the line of code exactly as written, substituting your parameter variable names in the proper places.
Avenue Functions:
 | The first Avenue option sends your parameters to a
central script called “Jennessent.DistFunc”, which checks for possible
errors in the parameters (using a negative value for Degrees of Freedom,
for example). If the script finds such values, it will halt operation
and alert you to the problem. If it doesn’t find errors, it forwards
your parameters to the appropriate script and returns the result to you.
Users may want to review the script “Jennessent.ProbDlogCalculate” for
an example of this option. IMPORTANT: Users should also be aware that
this script only checks to see if the input values follow the rules
described in the Discussions of Distribution Functions. It doesn’t check for basic errors such as
sending a non-numeric value to the script. |
| The second Avenue option is very similar to the first
in that it sends your parameters to a central script to check for errors
(“Jennessent.TableDistFunc” in this case), but it doesn’t halt operation
if it finds an error. Rather, it returns an error message (in String
format) detailing the problem. The author recommends this option for
cases in which the user wants to conduct calculations on a series of
values (i.e. records in a table), but doesn’t want the function to stop
if it finds an illegal value (possibly a record with no data). This
option would allow the user to insert an “if-then” statement in their
code to check if the result is a string or a number. Numerical responses
would indicate successful calculations while String responses could be
appended to a running report of unsuccessful calculations. Users may
want to review the script “Jennessent.ProbTabDlogCalculate” for an
example of this option. |
| If you’d like to skip the error-checking routines, use the third Avenue option to send your parameters to the relevant script directly. |
Discussion of Distribution Functions:
Probability Density Functions | Cumulative Distribution Functions |
Quantile Functions
Calculating Summary Statistics with Avenue
Back to Statistics/Distributions | Summary Statistics | References
Download Statistics Extension Manual (Adobe PDF)
Please visit Jenness Enterprises ArcView Extensions site for more ArcView Extensions and other software by the author. We also offer customized ArcView-based GIS consultation services to help you meet your specific data analysis and application development needs.
